View
탐색 알고리즘이란 수많은 데이터 중에서 원하는 데이터/값을 찾아내는 알고리즘이다.
검색 방법에 따라 두가지로 분류할 수 있다.
- 비교 검색 방식 : 검색 대상의 키를 비교하여 검색하는 방법 (ex. 트리 검색, 순차 검색, 이진 검색)
- 계산 검색 방식 : 계수적인 성질을 이용한 계산으로 검색하는 방법 (ex.해싱)
이진 검색 트리
검색 트리는 한 노드에서 최대 몇 개의 자식 노드로 분기를 할 수 있느냐에 따라 이진 검색 트리와 다진 검색 트리로 나뉨 (이진 검색 트리는 최대 두 개의 자식 노드를 가질 수 있다.)
이진 검색 트리는 다음과 같은 특징을 가진다.
- 각 노드는 키 값을 하나씩 갖는다. 각 노드의 키 값은 모두 달라야 한다.
- 최상위 레벨에 루트 노드가 있고, 각 노드는 최대 두 개의 자식 노드를 갖는다.
- 임의의 노드의 키 값은 자신의 왼쪽에 있는 모든 노드의 키 값보다 크고, 오른쪽에 있는 모든 노드의 키 값보다 작다.
이진 검색 트리에서 검색 (t : 검색할 트리의 루트 노드, x: 검색하고자 하는 키)
- 루트 노드 t의 키 값과 x를 비교해 x가 더 작으면 t의 왼쪽 서브 트리로 가서 x를 찾는다.
- x가 더 크면 t의 오른쪽 서브 트리로 가서 x를 찾는다.
treeSearch(t,x){
if(t = NIL or key[t]=x) then return t;
if(x < key[t])
then return treeSearch(left[t], x);
else return treeSearch(right[t], x);
}
순차 탐색
리스트 안에 있는 특정한 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법으로
- 보통 정렬되지 않은 리스트에서 데이터를 찾아야 할 때 사용
- 시간 복잡도 : O(N) 데이터 개수가 N개 일 때 최대 N번의 비교 연산이 필요
package search;
import java.util.Scanner;
public class search06 {
public static int sequantialSearch(int n, String target, String[] arr){
for(int i=0; i<n; i++){
if(arr[i].equals(target)){
return i+1;
}
}
return -1;
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
System.out.println("생성할 원수 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.");
int n = sc.nextInt();
String target = sc.next();
System.out.println("앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.");
String[] arr = new String[n];
for(int i=0; i<n; i++){
arr[i] = sc.next();
}
System.out.println(sequantialSearch(n, target, arr));
}
}
이진 탐색 ⭐⭐⭐
탐색 범위를 줄여, 원하는 데이터를 찾는 시간 복잡도를 O(logN)으로 줄여주는 알고리즘으로
- 배열 내부의 데이터가 정렬되어 있어야만 사용 가능
- 시간 복잡도 : O(logN) 한 번 확인할 때마다 확인하는 원소의 개수가 절반씩 줄어든다
이진 탐색 동작방식
- 위치를 나타내는 변수 3개 (시작점, 끝점, 중간점)을 사용하여 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교
1) 배열 / 시작점 / 끝점 / 찾고자하는 데이터 - 4개가 주어진다.
2) 시작점과 끝점의 중간점을 구한다.
3) 중간점이 가리키는 값이 찾고자하는 데이터면 끝
3-1) 중간점이 찾고자하는 데이터보다 크면 끝점을 중간점-1로,
3-2) 중간점이 찾고자하는 데이터보다 작다면 시작점을 중간점+1로 설정
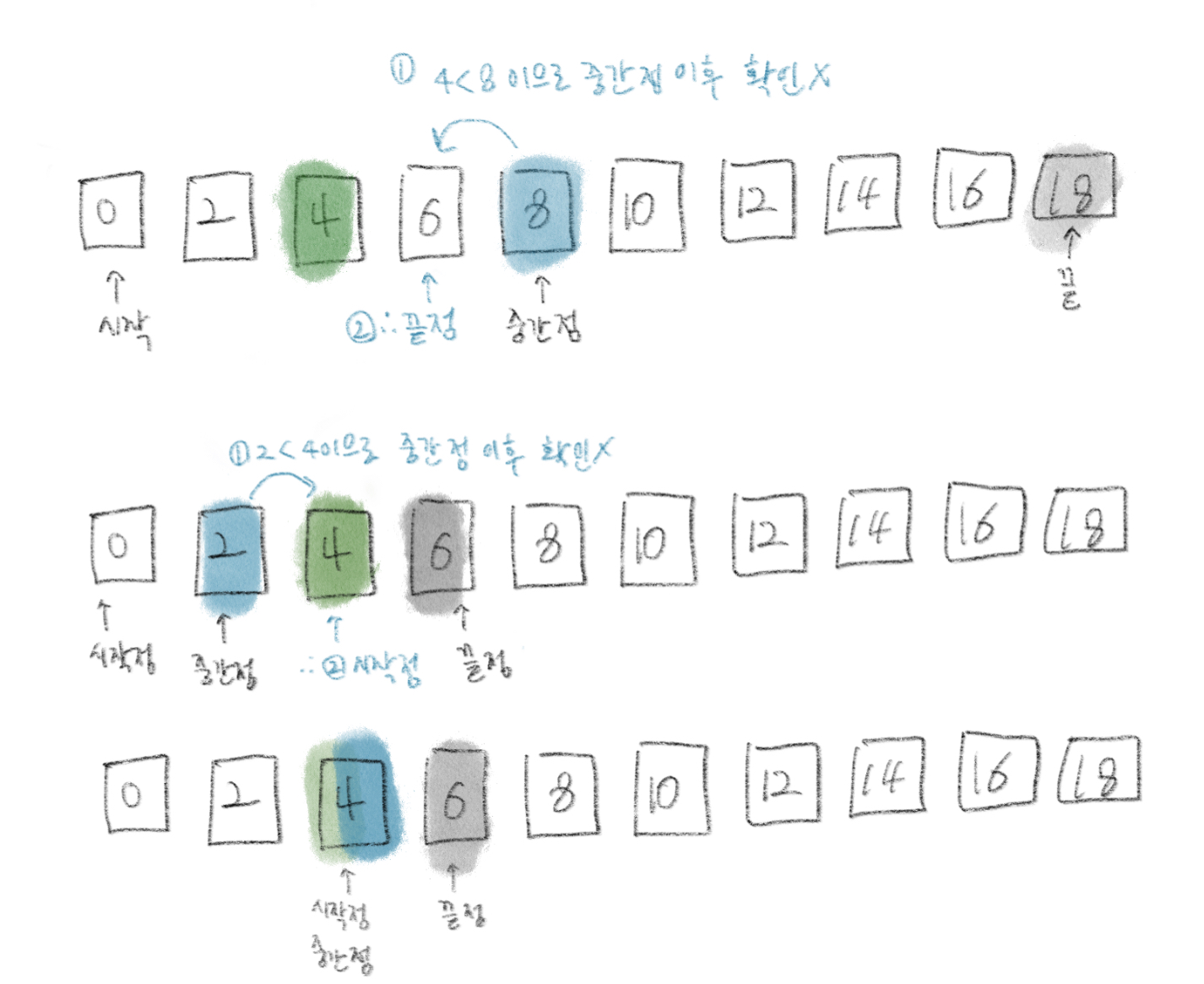
이진 탐색 구현방법
- 재귀 함수
package search;
import java.util.Scanner;
public class search07 {
public static int binarySearch(int[] arr, int target, int start, int end){
if(start > end) return -1;
int mid = (start + end)/2;
if(arr[mid] == target) return mid;
// 중간점의 값보다 작은 경우 왼쪽으로 끝점 이동
else if(arr[mid] > target) return binarySearch(arr, target, start, mid-1);
// 중간점의 값보다 큰 경우 오른쪽으로 시작점 이동
else return binarySearch(arr, target, mid+1, end);
}
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int target = sc.nextInt();
int[] arr = new int[n];
for(int i=0; i<n; i++){
arr[i] = sc.nextInt();
}
int result = binarySearch(arr, target, 0, n-1);
if(result == -1) System.out.println("원소가 존재하지 않습니다.");
else System.out.println(result+1);
}
}
- 반복문
public static int binarySearch(int[] arr, int target, int start, int end) {
while (start <= end) {
int mid = (start + end) / 2;
if (arr[mid] == target) return mid;
else if (arr[mid] > target) end = mid - 1;
else start = mid + 1;
}
return -1;
}
이진 탐색은 코딩 테스트에서 단골로 나오는 문제이니 가급적 외우길 권함
더불어 범위가 큰 상황에서의 탐색을 가정하는 문제에 많이 나온다.
처리해야 할 데이터의 개수나 값이 1000만 단위 이상으로 넘어가면,
이진 탐색과 같이 O(logN)의 속도를 내야 하는 알고리즘을 떠올려보자!
728x90
'알고리즘 > 이코테' 카테고리의 다른 글
| [이진 탐색] 이코테 정렬된 배열에서 특정 수의 개수 구하기(Java) (0) | 2022.12.10 |
|---|---|
| [이진 탐색] 이코테 고정점 찾기(Java) (0) | 2022.12.07 |
| [구현] 이코테 왕실의 나이트(Java) (0) | 2022.11.22 |
reply
