View
위상 정렬이란? 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것'
1) 진입차수가 0인 노드를 큐에 넣는다.
2) 큐가 빌 때까지의 다음의 과정을 반복한다.
⑴ 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
⑵ 새롭게 진입차수가 0이 된 노드를 큐에 넣는다.
💡 진입차수란? 특정한 노드로 들어오는 간선의 개수를 의미
이때 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재한다고 판단할 수 있다.
다시 말해 큐에서 원소가 V번 추출되기 전에 큐가 비어버리면 사이클이 발생한 것이다.
📍 알고리즘 동작 과정
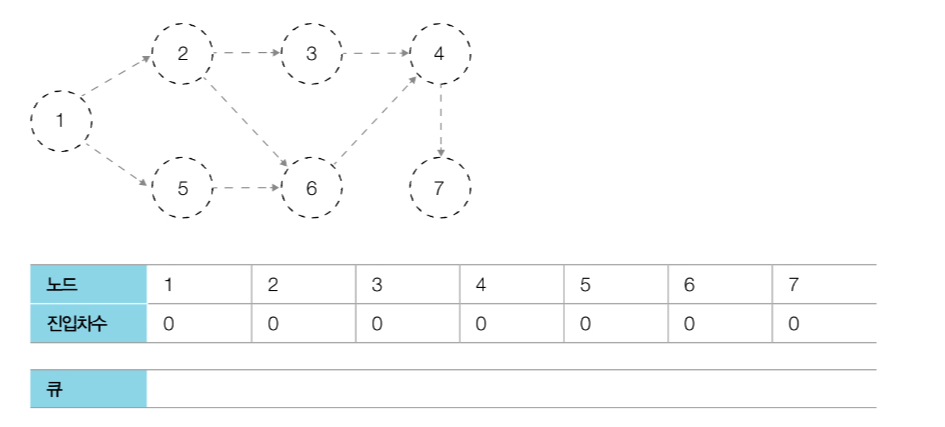
step0. 진입차수가 0인 노드를 큐에 넣는다.
현재 노드 1의 진입차수만 0이기 때문에 큐에 노드 1만 삽입

step1. 먼저 큐에 들어 있는 노드 1을 꺼낸 뒤 노드 1과 연결되어 있는 간선들을 제거한다.
그러면 새롭게 노드 2와 노드 5의 진입차수가 0이 된다. -> 노드 2와 노드 5를 큐에 삽입

step2. 큐에 들어있는 노드 2를 꺼낸 뒤 노드 2와 연결되어 있는 간선들을 제거한다.
그러면 새롭게 노드 3의 진입차수가 0이 된다. -> 노드 3을 큐에 삽입

.
.
.
step7. 큐에 들어있는 노드 7을 꺼낸 뒤 노드 7과 연결되어 있는 간선들을 제거한다.
새롭게 진입차수가 0이 되는 노드가 없으므로 그냥 넘어간다.
위 과정을 수행하는 동안 큐에서 빠져나간 노드를 순서대로 출력하면, 그것이 바로 위상 정렬을 수행한 결과가 된다.
(위상 정렬의 답안은 여러 가지가 될 수 있다.)
📍 소스코드
package graph;
import java.util.*;
public class graph09{
public static int v, e;
public static int[] indegree = new int[100001];
// 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// 위상 정렬 함수
public static void topologySort() {
ArrayList<Integer> result = new ArrayList<>(); // 알고리즘 수행 결과를 담을 리스트
Queue<Integer> q = new LinkedList<>(); // 큐 라이브러리 사용
// 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for (int i = 1; i <= v; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
// 큐가 빌 때까지 반복
while (!q.isEmpty()) {
// 큐에서 원소 꺼내기
int now = q.poll();
result.add(now);
// 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for (int i = 0; i < graph.get(now).size(); i++) {
indegree[graph.get(now).get(i)] -= 1;
// 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if (indegree[graph.get(now).get(i)] == 0) {
q.offer(graph.get(now).get(i));
}
}
}
// 위상 정렬을 수행한 결과 출력
for (int i = 0; i < result.size(); i++) {
System.out.print(result.get(i) + " ");
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
e = sc.nextInt();
for (int i = 0; i <= v; i++) {
graph.add(new ArrayList<Integer>());
}
// 방향 그래프의 모든 간선 정보를 입력 받기
for (int i = 0; i < e; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
graph.get(a).add(b); // 정점 A에서 B로 이동 가능
// 진입 차수를 1 증가
indegree[b] += 1;
}
topologySort();
}
}위상 정렬의 시간 복잡도 : O(V+E)
📚 실전문제
동빈이는 온라인으로 컴퓨터 공학 강의를 듣고 있다. 이 때 각 온라인 강의는 선수 강의가 있을 수 있는데, 선수 강의가 있는 강의는 선수 강의를 먼저 들어야만 해당 강의를 들을 수 있다. 동빈이는 총 N개의 강의를 듣고자 한다. 강의는 1번부터 N번까지의 번호를 가진다. 또한 동시에 여러 개의 강의를 들을 수 있다고 가정한다. 예를 들어, N = 3일 때, 3번 강의의 선수 강의로 1번과 2번 강의가 있고, 1번과 2번 강의는 선수 강의가 없다고 하자. 그리고 각 강의에 대하여 강의 시간이 다음과 같다고 하자.
1번 강의: 30시간
2번 강의: 20시간
3번 강의: 40시간
이 경우, 1번 강의를 수강하기까지의 최소 시간은 30시간, 2번 강의를 수강하기까지는 최소 20시간, 3번 강의를 수강하기까지는 최소 70시간이 필요하다. 동빈이가 듣고자 하는 N개의 강의 정보가 주어졌을 때, N개의 강의에 대하여 수강하기까지는 걸리는 최소 시간을 출력하는 프로그램을 작성해라.


📝 문제 해설

각 노드(강의)에 대하여 인접한 노드를 확인할 때, -> 진입차수가 0인 노드를 큐에 넣고 큐가 빌 때까지 반복
인접한 노드에 대하여 현재보다 강의 시간이 더 긴 경우가 있을 때마다 더 오랜 시간이 걸리는 경우의 시간을 저장하여 결과 테이블을 갱신하여 답을 구할 수 있음
while (!q.isEmpty()) {
int now = q.poll();
for (int i = 0; i < graph.get(now).size(); i++) {
result[graph.get(now).get(i)] = Math.max(result[graph.get(now).get(i)], result[now] + times[graph.get(now).get(i)]);
indegree[graph.get(now).get(i)] -= 1;
if (indegree[graph.get(now).get(i)] == 0) {
q.offer(graph.get(now).get(i));
}
}
}package graph;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class graph10 {
public static int v;
public static int[] indegree = new int[501]; // 진입차수
public static int[] times = new int[501]; // 각 강의 시간
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>();
// 위상 정렬 함수
public static void topologySort() {
int[] result = new int[501]; //최소 시간을 담는 결과 테이블
for(int i=1; i<=v; i++){
result[i]=times[i];
}
Queue<Integer> q = new LinkedList<>();
for (int i = 1; i <= v; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
while (!q.isEmpty()) {
int now = q.poll();
for (int i = 0; i < graph.get(now).size(); i++) {
result[graph.get(now).get(i)] = Math.max(result[graph.get(now).get(i)], result[now] + times[graph.get(now).get(i)]);
indegree[graph.get(now).get(i)] -= 1;
if (indegree[graph.get(now).get(i)] == 0) {
q.offer(graph.get(now).get(i));
}
}
}
// 위상 정렬을 수행한 결과 출력
for (int i = 1; i <= v; i++) {
System.out.println(result[i]);
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
v = sc.nextInt();
for (int i = 0; i <= v; i++) {
graph.add(new ArrayList<Integer>());
}
for (int i = 1; i <= v; i++) {
int x = sc.nextInt();
times[i] = x;
while(true){
x = sc.nextInt();
if ( x == -1) break;
indegree[i] += 1;
graph.get(x).add(i);
}
}
topologySort();
}
}
'알고리즘 > 이코테' 카테고리의 다른 글
| [그리디] 이코테 모험가 길드(Java) (0) | 2022.07.26 |
|---|---|
| 10. 그래프 이론 - 서로소 집합 (0) | 2022.07.22 |
| 09. 최단 경로 - 다익스트라 최단 경로 알고리즘 (0) | 2022.07.11 |
