View
📚 문제
손님이 왔을 때 요청한 총 길이가 M일 때 적어도 M만큼의 떡을 얻기 위해 절단기에 설정할 수 있는 높이의 최댓값을 구하는 프로그램을 작성하시오

📝 문제 해설
: 적절한 높이를 찾을 때까지 절단기의 높이 H를 반복해서 조정하는 것
전형적인 이진 탐색 문제이자, 파라메트릭 서치 유형의 문제이다.
이 높이 괜찮아..? 를 확인한 뒤에 조건의 만족 여부에 따라서 탐색 범위를 좁혀서 해결할 수 있다.
범위를 좁힐 때는 이진 탐색의 원리를 이용한다!
💡 파라메트릭 서치
최적화 문제를 결정 문제('예' 혹은 '아니오'로 답하는 문제) 로 바꾸어 해결하는 기법
-원하는 조건을 만족하는 가장 알맞은 값을 찾는 문제에 주로 사용
- 예를 들어 범위 내에서 조건을 만족하는 가장 큰 값을 찾으라는 최적화 문제라면 이진 탐색으로 결정 문제를 해결하면서 범위를 좁혀갈 수 있다.
(참고 : https://sarah950716.tistory.com/16 )
절단기의 높이(탐색 범위)는 1부터 10억까지의 정수 중 하나임. 이처럼 큰 수를 보면 무지성으로 이진 탐색을 떠올려야함
절단기의 높이 H는 0부터 가장 긴 떡의 길이 안에 있어야만 떡을 자를 수 있다.
중간점의 값은 시간이 지날수록 '최적화된 값'을 찾기 때문에
과정을 반복하면서 얻을 수 있는 떡의 길이 합이 필요한 떡의 길이보다 크거나 같을 때마다 중간점 값으로 갱신해주면 된다.
i) 시작점은 0, 끝점은 가장 긴 떡의 길이 19로 설정 : 절단기의 높이(중간점) : 9
얻을 수 있는 떡의 합은 25로 필요한 떡의 길이보다 큼 > 시작점 증가

ii) 시작점은 10, 끝점은 가장 긴 떡의 길이 19로 설정 : 절단기의 높이(중간점) : 14
얻을 수 있는 떡의 합은 9로 필요한 떡의 길이보다 큼 > 시작점 증가

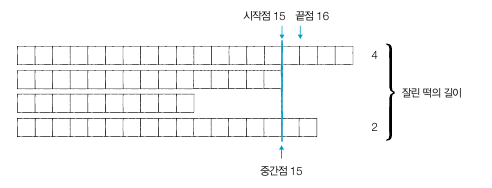
iii) 시작점은 15, 끝점은 가장 긴 떡의 길이 19로 설정 : 절단기의 높이(중간점) : 17
얻을 수 있는 떡의 합은 2로 필요한 떡의 길이보다 작음 > 끝점 감소

iv) 시작점은 15, 끝점은 16으로 설정 : 절단기의 높이(중간점) : 15
얻을 수 있는 떡의 합은 6
1. 잘라낸 떡이 M과 일치 : 현재 절단기 높이 반환
2. 잘라낸 떡이 M보다 작을 경우 : 절단기 길이 줄임
3. 잘라낸 떡이 M보다 클 경우 : 절단기 길이 늘림
- 다만, 끝내 M과 일치하도록 자를 수 없는 경우를 대비하여 현 높이(max)를 저장
import java.util.*;
public class search11 {
static int n,m;
static int[] arr;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = sc.nextInt();
}
Arrays.sort(arr);
System.out.println(binarySearch(arr, m));
}
public static int binarySearch(int[] arr, int target) {
int start = 0;
int end = arr[n-1];
int max = 0;
while(start <= end) {
int mid = (start+end)/2;
int total = 0;
for(int i : arr) {
total += Math.max((i-mid), 0);
}
if(total == m) {
return mid;
}else if(total < m) {
end = mid-1;
}else {
start = mid+1;
max = mid;
}
}
return max;
}
}'알고리즘 > 이코테' 카테고리의 다른 글
| [알고리즘] 08. 동적 계획법(Dynamic Programming) (0) | 2022.06.30 |
|---|---|
| [이진 탐색] 이코테 부품 찾기(Java) (0) | 2022.06.29 |
| [정렬] 이코테 성적 출력(Java) (1) | 2022.06.21 |
